미분의 뒷이야기 - 미분은 왜 배울까?

오늘 장장 3시간의 강의를 들으면서 “미분은 왜 배울까?”라는 생각이 드셨을 수도 있습니다.

흔히 고등학교 교과과정에서 “미분은 그냥 기울기다”라고만 배우면, 접선의 기울기를 구하는 게 도대체 무슨 쓸모가 있는지 궁금하실 겁니다.

사실 본질적으로 그래프의 접선의 기울기를 구한다는 것은 두 변수 간의 관계를 구한다는 것입니다.

1. 미분의 본질적인 의미 - 미분은 “두 변수의 변화율의 관계”

예를 들면 시간 t(초)에 따라 특정 지점으로부터의 거리가 t^2(m) 으로 변하는 차가 있다고 할 때, 

거리는 t에 대한 함수이므로 x(t) = t^2 이라고 쓸 수 있습니다. (함수는 f라고 쓴다고 배웠지만, 거리를 x로 쓰니까 함수 이름도 그냥 x라고 쓰는 게 보편적입니다.)

t = 1, 즉 1초일 때의 속력을 구한다는 것은 t = 1 일 때 “시간이 변할 때 거리가 얼마나 빠르게 변하는가?”를 구한다는 것입니다.

예를 들어 t = 1.01 일 때 거리는 (1.01)^2 = 1.0201 이고, t = 1.001 일 때 거리는 (1.001)^2 = 1.002001 이고, … 이렇게 계산됩니다.

즉, 시간이 0.01초 변할 때 거리는 0.0201m, 시간이 0.001초 변할 때 거리는 0.002001m … 로 변한다는 뜻이고,

이는 곧 시간 간격이 짧아질 수록, 시간에 대한 거리의 변화율의 비가 2에 가까워진다는 뜻이죠.

이것을 거리의 시간에 대한 “순간변화율” 이라고 합니다. 미분에서 배웠던 순간변화율과 연결되는 것이죠.

이 때 거리와 시간의 그래프를 그려보면 그래프의 t=1에서의 접선의 기울기가 바로 거리의 시간에 대한 순간변화율이니까 

접선의 기울기가 순간변화율과 연결되는 것입니다.

이 때 순간 변화율의 의미는  t=1 근처에서 (x변화량)/(t변화량)으로 구할 수 있고, 변화량이 엄청 작다는 의미에서

dx/dt라고도 표기합니다. (이건 그저 약속된 표기일 뿐이니 d를 약분한다거나 그러면 안됩니다^^ d는 특수 기호 같은 거라고 생각하면 됩니다)

2. 미분법 - 함수의 변화율을 빠르게 구할 수 있다

t = 1에서 거리 x(t) = t^2 의 순간변화율이 2라는 것을, 아까 전에 t = 1.01, 1.001 이렇게 일일이 대입해서 구했는데,

“미분법”이라는 것을 배우면 이걸 일일이 대입하지 않고 바로 계산할 수 있습니다.

승제쌤 수업 마지막에 t^2을 미분하면 2t가 나온 것을 유도했는데, 이걸 알고 있다면 

이제 일일이 t를 대입하지 않고도 t = 1에서 순간변화율은 2구나! 를 알 수가 있는 것이죠.

t^2 같은 간단한 함수 뿐만 아니라, 수학자들은 연구를 통해서 우리가 알고 있는 유용한 함수들에 대해서 전부 미분법을 개발해놨습니다.

sinx를 미분하면 cosx, cosx를 미분하면 -sinx 이런 식으로 말이죠. 

(아알 분의 와아이는 사아인함수~ 할 때 그 sin함수 맞습니다)

즉, f(t) = t^2 과 같이 변하는 함수 뿐만 아니라 별의 별 이상한 함수가 나와도 우리가 이미 미분법을 알고 있는 함수라면,

순간변화율을 바로 구할 수 있다는 것입니다. t에다 자잘한 숫자를 대입하지 않고도 말이죠!

3. 여러 변수 간의 변화율

예를 들어 아래 그림처럼 빛에 의해 공의 그림자가 생기는 상황에서, 공이 움직일 때 그림자의 속력을 구하고 싶다고 해봅시다.

광원에서 공까지의 거리와 공에서 그림자까지의 거리가 같을 때, 공이 3m/s 로 움직인다면 그림자는 어떤 속도로 움직이게 될까요?

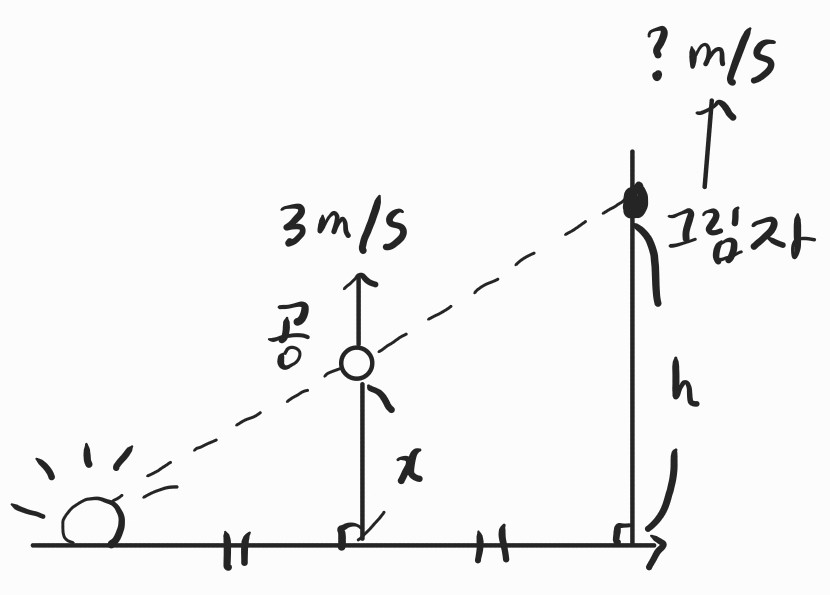
닮음비에 의해서 h = 2x다, 따라서 답이 6m/s 라는 것이 바로 보였다면, 합성함수의 미분을 이미 이해하고 있는 겁니다.

t : 시간, x : 공의 높이, h : 그림자의 높이라고 했을 때,

공이 3m/s 로 움직인다 : 공 높이의 시간에 대한 변화율 = dx/dt = 3

공이 움직일 때 그림자는 2배로 빨리 움직인다 (feat. 닮음비) : 그림자 높이의 공 높이에 대한 변화율 = dh/dx = 2

그림자 높이의 시간에 대한 변화율 = dh/dt = 3x2 = 6

즉, 아래 관계가 성립하게 됩니다.

x는 t에 대한 함수, h는 x에 대한 함수이니까 h는 t에 대한 합성함수 꼴로 나타나는 것이고,

이게 사실상 이과에서 배우는 합성함수 미분, 더 나아가 “여러 변수의 관계”인 것이죠.

이를 이용해 우리는 여러 변수가 아무리 복잡하게 얽혀 있어도 아래와 같이 변화율을 구할 수 있습니다.

두 변수의 관계를 여러 변수의 관계로 확장하는 것이죠.

이와 같이 여러 변수의 관계를 식으로 세우고, 이 변수들 간의 변화율의 관계를 “미분” 하나로 계산할 수 있다보니 쓰임새가 너무나도 많습니다.

날짜에 따른 기온 변화 → 기온에 따른 아이스크림 판매량의 변화 → 판매량에 따른 수익의 변화

시간에 따른 천체의 위치의 변화 → 천체의 위치에 따른 중력의 변화 → 중력에 따른 가속도의 변화

이 외에도 대학 미적분학 책에 예제로써 단골소재로 등장하는 거리의 변화량 문제, 물이 그릇에서 빠져나가는 속도 문제,

최단 거리 계산, 최적 경로 찾기 등등 최적화문제, 궤도 계산, 과속 단속 층정기 등등

수학이 사용되는 공학/과학에서는 미분이 안 쓰이는 분야가 거의 없을 정도죠.

미분 이전에 멈춰있던 세상만 볼 수 있었지만, 미분 이후에 세상을 구성하는 여러 변수들간의 관계를 파악할 수 있게 되면서,

비로소 움직이는 세상을 볼 수 있게 된 것이죠.

데카르트의 좌표계와 뉴턴-라이프니츠의 미적분학 이후 수학이 발전하고 그에 따라 과학혁명이 시작되었다는 말도 있고, 

미적분학이 수학의 꽃이라는 말도 있는 것듯이 미분은 너무 중요한 개념입니다.

저도 수학과를 졸업하고 수학을 가르치고 있는 입장인데 침착맨님이 오늘 수업처럼 집중하고 또 여러 가지로 관통하는 모습을 보니까 

제가 다 뿌듯하네요ㅋㅋ