버츠와 스위너톤-다이어 추측에 대해서 araboza

정수론민수가 들려주는 버츠와 스위너톤-다이어 추측

흔히 수학의 가장 유명한 문제들로는 100만불 상금이 걸려있는 밀레니엄 문제가 있지. 그 중 가장 유명한 문제가 바로 리만 가설이 아닐까 싶어. 궤도님께서도 안될 과학에서 다뤄주셨고. 그 다음으로 유명한 문제는 아마 푸앵카레 추측이 아닐까? 밀레니엄 문제 중 유일하게 해결된 문제니까.

이번 시간엔 밀레니엄 문제 중에서 상대적으로 덜 유명하지만, 내가 연구하는 분야와 굉장히 깊은 연관이 있는 문제인 버츠와 스위너톤-다이어 추측을 소개해볼까 해.

먼저 들어가기에 앞서 버츠와 스위너톤-다이어 추측은 버츠 라는 수학자와 스위너톤-다이어라는 수학자가 만든 추측이야. 그래서 '버츠'와 '스위너톤-다이어'추측인 것이지. 흔히 줄여서 BSD 추측, 혹은 BSD라고 불려.

BSD의 전문은 다음과 같아.
 

K/Q가 수체이고, E/K가 타원곡선일 때 E(K)의 대수적 계수는 해석적 계수, 즉 E의 하세-베유 함수 L(E,s)의 s=1에서의 테일러 전개했을 때, (s-1)의 최소 차수와 같다.

아니 이게 다 뭔소리람. 사실 BSD의 전문을 이해하는 데에는 어려우니까 가장 기본적인 케이스에 대해서만 다뤄볼게.

1. 유한생성과 무한생성

먼저 자연수를 생각해보자. {1,2,3,4,...}. 여기서 +를 얼마든지 사용할 수 있다면, 자연수를 모두 만들어내는데 필요한 수는 무엇일까? 바로 1이야. 예를 들어 
2 = 1+1
3 = 1+1+1
4 = 1+1+1+1
등등, 1과 +가 얼마든지 있다면 어떤 수든 만들어낼 수 있지. 이 경우 '자연수는 덧셈에 대해서 유한생성이다'라고 해. 자연수를 모두 만들어내는데에는 유한개의 원소(정확히는 1개의 원소)만 있으면 된다는 것이지.

그렇다면 곱셈인 경우는 어떨까? 곱하기를 얼마든지 이용할 수 있다는 가정하에 모든 자연수를 만드는데 필요한 숫자의 개수는 몇 개일까? 덧셈과 같이 1부터 볼까? 1은 얼마든 곱해도 항상 1이야. 그래서 1로는 자연수를 만들어내긴 택도 없이 부족하지.

1과 2로는 어떨까? 조금 더 많은 숫자들을 만들 수 있겠지? 하지만 아무리 노력해도 만들어낼 수 있는 수는 1과 모든 2의 제곱수들 뿐일거야.

1, 2, 3으로는? 2의 제곱수도, 3의 제곱수도 만들어낼 수 있겠지. 2의 제곱수와 3의 제곱수의 곱꼴의 형태의 숫자들도 만들어낼 수 있을거야, 예컨대 6, 12, 18, 24, 등등. 하지만 여전히 모든 숫자들을 만들어내긴 턱없이 부족하지.

사실 자연수를 곱셈으로 모두 만들어내는데에는 모든 소수들이 필요해. 소수는 무한히 많다는 것이 증명되었으니, '자연수는 곱셈에 대해 무한생성이다'라고 말할 수 있겠지.

연습 문제) 모든 유리수는 덧셈에 대해서도, 곱셈에 대해서도 무한 생성임을 보이시오. (유리수란, 모든 분수들을 말한다.)

2. 타원곡선

다음과 같은 방정식을 보자.

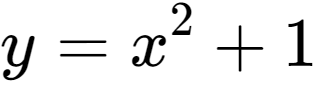
이 식을 만족하는 x와 y는 무궁무진하게 많아. (0,1)도 되고, (√2,3)도 있을 수 있겠지. 이 때 (x,y)에서 x와 y가 둘 다 유리수인 경우를 유리점이라고 부르도록 하자. 방금 예의 경우 (0,1)은 유리점이야. 0과 1은 정수고, 모든 정수는 유리수거든. 반면 (√2,3)은 유리점이 아니야. 설령 3은 유리점이더라도 √2는 유리수가 아니니까.

또 다른 예제를 볼까?

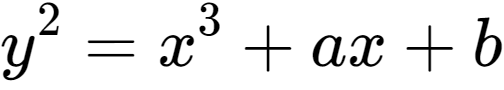
이와 같은 꼴의 식을 타원곡선이라고 해. 여기서 a와 b는 유리수야. 단, 조금 기술적인 문제로 4a^3+27b^2은 0이 아니어야 한다는 조건이 붙지. 이 식을 토대로 그래프를 그려보면 다음과 같아.

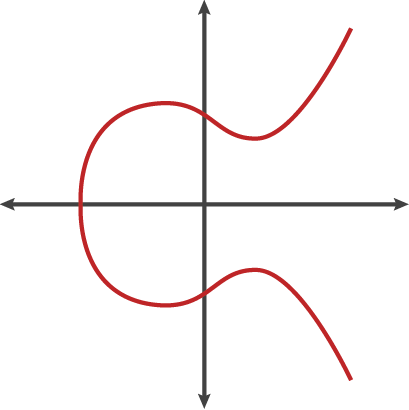
(이렇게 하나의 곡선인 경우도 있지만, 두개의 곡선으로 분리된 형태도 있어.)

타원 곡선은 '두 점을 갖고 연산을 취해줄 수 있다'라는 아주 특이한 성질이 있어. 처음 연산 방식을 보면 '아니 뭐 저렇게 이상하게 정의되었대? 싶을 수 있지만... 자세한 이유를 설명하면 너무 복잡해지니 그러려니 해줘.

타원 곡선에서 덧셈 정의하는 법

1. P라는 점과 Q라는 점이 타원곡선 위에 있다고 치자. 
2. P와 Q를 연결하는 직선을 그린다. (만약 P와 Q가 '같은 점'이라면 P를 지나는 접선을 그린다.)
3. P와 Q가 정확히 서로의 위 아래에 있지 않다면, 그 직선은 타원곡선과 또다른 지점에서 만날 것이다. 해당 점을 -R이라고 하자.
4. -R를 지나는 수직선을 그린다. 이 선은 타원곡선과 만난다. 그 점을 R이라고 하자.
5. P라는 점과 Q라는 점의 합, 즉 P+Q를 R이라고 정의한다.

이것을 편의상 ‘이상한 덧셈’이라고 부르자. (수학자들은 그냥 '타원곡선 상에서의 덧셈'이라고 불러.)

이 굉장히 이상한 덧셈은 '특이한' 성질이 있어, 바로 타원곡선의 두 점 P와 Q가 유리점이었다면, P+Q점 역시 유리점이라는 성질이야.

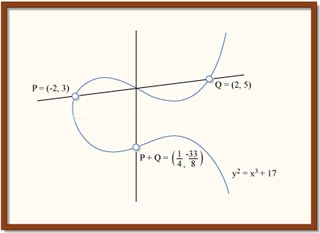
예시로 붙인 그림이 조금 화질구지인데… y^2 = x^3+17 이라는 타원 곡선이야.

잘 보면 P = (-2,3)이고, Q = (2,5)이야. 정수는 유리수이므로, P와 Q 둘 다 유리점이지. 

둘 사이를 연결하는 직선 (검은색 가로선)은 타원곡선 (파란색 곡선)과 만나지? 그림에선 표기되지 않았지만, 그 점이 -R이야.

-R을 기준으로 내린 수직선이 타원 곡선과 만나는 점이 곧 P+Q인데 이 점은 (1/4, -33/8)이야. 1/4도, -33/8도 유리수니까, 이 점도 유리점이지.

이처럼 타원 곡선 위엔 P와 Q가 유리점이라면 P+Q는 항상 유리점이야.

자 그럼 처음의 유한생성/무한생성의 문제로 돌아와보자.

자연수는 덧셈에 대해서 유한생성이었어, 1과 덧셈만 있으면 '모든' 자연수를 만들어낼 수 있으니까.

그렇다면 타원곡선의 유리점들은 방금 정의한 덧셈에 대해서 유한생성일까? 무한생성일까? 베유라는 수학자가 이에 대한 답을 찾았지.

'타원곡선의 유리점들은 항상 유한생성이다.'

유리점이 하나도 없는 타원 곡선도 있고, 유한개의 유리점을 가진 타원 곡선도 있어. 심지어 무한개의 유리점을 가진 타원 곡선도 있지. 하지만 뭐가 됐든, 타원곡선의 모든 유리점은 '항상' 유한 생성이야. 즉 '몇 개의 유리점'만 갖고, 앞서 소개된 '이상한 덧셈'을 사용하면 모든 유리점들을 찾아낼 수 있다는 것이지.

조금 어려운 내용이지만, 다른 곡선들에 대한 이야기도 잠깐 해볼게. 곡선들은 ‘종수’라는 개념으로 분류할 수 있어.

예를 들어 y^2 + x^2 = 1이라는 '원의 방정식'은 종수가 0인 곡선이야. 앞서 소개한 타원곡선은 종수가 1인 곡선이지. 그 외에도 종수가 2인 곡선, 종수가 3인 곡선 등 얼마든지 만들어낼 수 있어. 마찬가지로 각 곡선마다 '유리점'들에 대해 연구할 수 있지. 여기에 대해 수학자들이 알아낸 바에 따르면...

종수가 0인 곡선은 유리점이 하나도 없을 수도 있고, 유한히 많을 수도 있고, 무한히 많을 수도 있다. 이들을 '모두' 찾아내는 방법은 알려져 있다.

종수가 1인 곡선은 유리점이 하나도 없을 수도 있고, 유한히 많을 수도 있고, 무한히 많을 수도 있다. 하지만 '항상' 유한생성이다. 이들을 '모두' 찾아내기란 굉장히 어렵다.

종수가 2 이상인 곡선은 유리점이 하나도 없을 수도 있고, 유한히 많을 수도 있다. 하지만 '절대로 무한히 많을 수는 없다.' 이들을 '모두' 찾아내기란 극단적으로 어렵다.

정말 온 세상이 종수인 것인가… 모든 곡선은 종수로 결정된다…

자, 우리의 초점은 타원곡선, 즉 종수가 1인 곡선이야. 말했다시피, 타원곡선의 유리점은 항상 유한생성이지. 몇 개의 유리점만 있으면 모든 유리점들을 찾아낼 수 있어. 편의상 이 점들을 P1, P2, ..., Pn 이라고 하자.

이들 중 '어떤 유리점'들은 여러번 스스로 더하다보면 (∞, ∞)꼴이 나와. 예컨대 앞서 소개한 '이상한 덧셈' 규칙을 사용해서 P1 + P1 + ... + P1 하고 여러번 더하다 보면 언젠가 (∞, ∞)가 되어. 이런 점은 '꼬인 점'이라고 불려. 이런 점들은 최대 2개 뿐이라는 사실은 이미 알려져 있어. 즉 P1, …, Pn 중에는 꼬인점이 1개도 없거나, 1개 거나, 2개라는 것이지.

하지만 꼬인 점이 아닌 점들은 제 아무리 더해도 (∞, ∞)가 나오지 않아. 이 점을 '자유점'이라고 하자. 이 자유점의 개수가 바로 타원곡선의 '대수적 계수'야. 

3. 해석적 계수

이 부분은 조금 예시없이 두루뭉술하게 설명할게. (앞서 소개한것보다 훨씬 어려운 내용이라...)

제타 함수라는 함수가 있지? 바로 그 유명한 리만 가설에서 다루는 함수야.

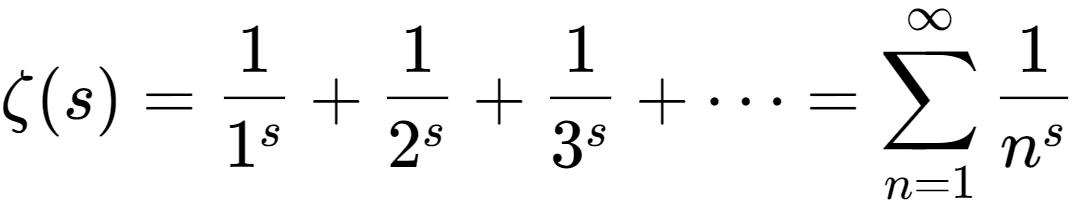
보다시피 모든 자연수의 s승의 역수들의 합이라, 정수를 연구하는데에는 굉장히 중요한 함수지.

하지만 이 제타 함수는 L-함수라는 이름의 확장팩이 그것도 여러개나 있어. 대표적인 예로는 디리클레 L-함수, 보형 L-함수, 아틴 L-함수, 헤케 L-함수, 하세-베유 L-함수 등이 있지. 뭐가 많지만, 그래도 기본적인 틀은 같아. ‘제타 함수를 조금 더 다양한 환경에서 정의해보자’라는 기준으로 만들었다는 것이지.

왜 이런 다양한 L-함수들이 나왔나? 그건 다양한 분야들 사이에 발견하지 못했던 연결고리를 찾기 위해서야. 이른바 수학판 대통일장 이론인 셈이지. 랭글랜즈라는 수학자가 처음으로 제시한 목표라서 랭글랜즈 프로그램이라고 불려. 얼마나 원대한 목표인지 가늠할만한 설명으로 뭐가 있을까… 아래 그림이 랭글랜즈 프로그램의 도식인데, 빨간색에서 노란색으로 가는 화살표 Modularity가 바로 앤드류 와일즈가 페르마의 마지막 정리를 증명하기 위해 만들어낸 정리야. 그 위대한 업적이 고작 저 화살표 하나에 불과한 셈이지.

어쨌든 다시 본론으로 돌아와서, 앞서 소개한 L-함수 중 '타원 곡선판 DLC'가 있는데, 바로 하세-베유 L-함수가 그것이야. 흔히 L(E,s)라고 표현하는데, E는 타원곡선을, s는 변수를 의미하지.

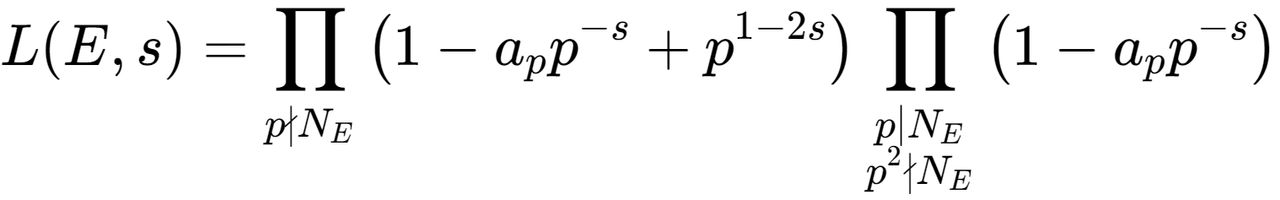
L(E,s)에 s = 1을 대입하면, 두 가지 경우의 수를 생각해볼 수 있어. 0이 나온다, 0이 안 나온다. 먼저 0이 나오지 않는 경우에 대해 BSD는 이렇게 말하고 있어.

L(E,1)이 0이 아니라면, 타원곡선 E는 '자유점'이 없다. (다시 말해, E의 모든 유리점은 최대 2개의 꼬인 점으로 모두 생성이 가능하다.)

반면 L(E,1)이 0이라면, 얼마나 빠르게 0으로 수렴하는지를 계산해야 해.

예를 들어 y = x 라는 식과 y = x^2라는 식을 보자.

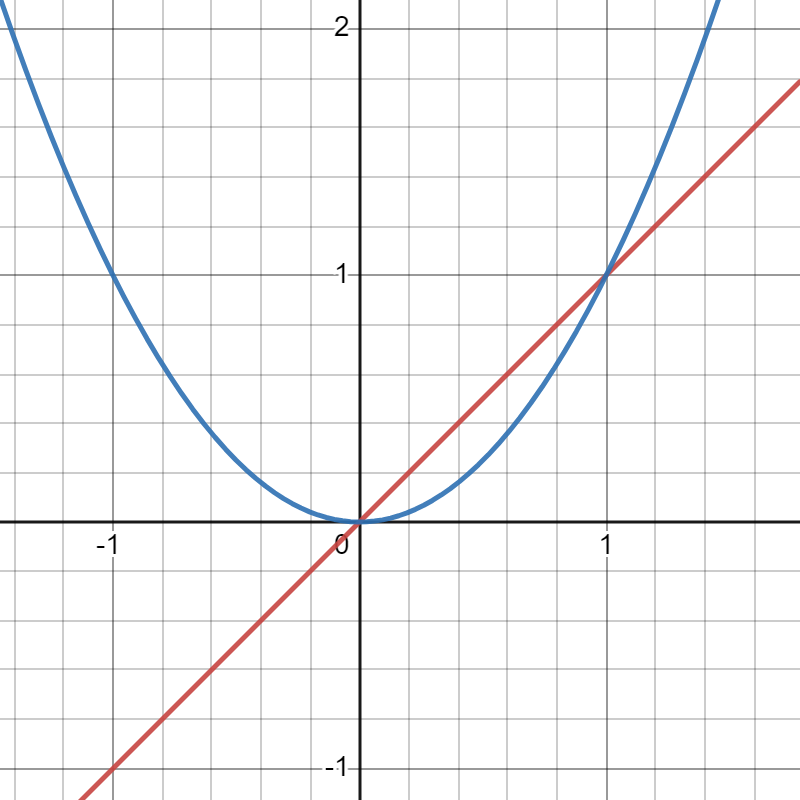
y = x라는 식(빨강)도, y = x^2라는 식(파랑)도 둘 다 x에 0을 대입하면 0이 돼. 하지만 그래프를 보다시피 y = x보다 y = x^2가 0에 훨씬 더 빠르게 다가가지. 그 근본적인 차이는 바로 x의 차수에 있어. 일반적으로 x의 차수가 ‘클수록’ 0으로 더 빨리 다가가지. 

마찬가지로 L(E,1) = 0이라면, s = 1에 다가갈수록, L(E,s)는 0으로 다가간다는 뜻이야. E가 어떤 타원곡선이냐에 따라 ‘느긋느긋’하게 0에 다가가는 애들도 있고 ‘호다다닥’ 0에 다가가는 애들도 있어. 전자는 차수가 낮은 것이고 후자는 차수가 높은 것이지. 이 차수를 ‘해석적 계수’라고 불러.

BSD는 L(E,1) = 0인 경우에는 다음과 같이 말해.

L(E,1) = 0이라면, E는 자유점이 있다. 그 자유점의 개수는 해석적 계수, 즉 L(E,s)가 얼마나 빠르게 0으로 수렴하는가의 정도와 일치한다.

요약하자면 BSD의 내용은 다음과 같아.

1. 타원곡선의 유리점은 유한할 수도 있고 무한할 수도 있다. 
2. 타원곡선의 유리점을 이상한 덧셈을 통해 모두 만들어주는 '특별한 점'들이 있다. 이 점들은 무조건 유한개이다.
3. 하지만 이 ‘특별한 점’들의 개수는 계산해내기가 굉장히 어렵다.
4. 반면 타원곡선을 기반으로 L함수라는 함수를 만들어낼 수 있다. 
5. 이 함수는 1을 대입했을 때 0이 된다면 특별한 점 중 자유점은 없는 것으로 추측된다. 0이 된다면, 특별한 점 중 자유점이 있는 것으로 추측된다.
6. 심지어 얼마나 빠르게 0으로 가는지를 기반으로 자유점의 개수를 파악할 수 있는 것으로 추측된다.

이렇게 오늘은 BSD에 대해서 설명해봤어. 사실 나름 쉽게 쓴다고 노력은 해봤지만… 대학원 수준의 정수론 수업을 들어야 이해할 수 있는 내용이라, 많은 부분은 잘라내거나 설명을 대충 했어. 하지만 그래도 ‘아 타원 곡선의 유리점을 파악하기 위한 똥꼬쇼로군’ 정도로 이해하면 될 것 같아. 오늘의 교훈은

1. BSD는 개어렵다.
2. 온 세상이 종수다.
3. 타원곡선 짱짱맨