상대성이론이 쓰는 미분기하학이 뭔데!

안녕하세요, 처음 글 쓰는 수학준수입니다 :)

수학과 과학에 관심이 많으신 여러분들을 보고 ‘언젠가는 글을 써야지’라는 생각만 하고 살았는데요.

원래 바쁠 때 보는 침투부가 제일 재미있듯 가장 바쁜 지금에야 글을 쓰게 되었네요.

첫 글이니만큼 과학과 관련된 수학을 소개하고자 (일반)상대성이론에 사용되는 미분기하학을 들고 와봤습니다!

저는 학부생이라 정보가 틀릴 수도, 미흡할 수도 있으니 많은 지적과 질문은 환영입니다 :)

서론이 길었네요.

기하학이면 기하학이지. 미분기하학은 또 뭐야?

라고 느끼실 여러분들을 위하여 ‘미분’이 어떤 의미를 갖는지 조금 알아보도록 합시다.

미분을 왜 할까요?

과학을 공부하시는 많은 분들께 익숙한 미분은

속도나 가속도 등을 이용하면 거꾸로 위치같은 물리량을 알 수 있다!

일 것 같네요.

이 답변은 미분을 이해하는 하나의 방법으로 아주아주 훌륭한 접근입니다.

주로 ‘미분방정식론’ 등의 분야에서 주로 이용하는 접근이죠.

근데 미분기하학이 갖는 접근은 사뭇 다릅니다.

내가 사는 (시)공간이 어떻게 생겨먹었는지 모르겠는데?

이게 첫 질문이죠. 자, 이제 그럼 어떻게 해야 이 질문을 해결할 수 있을까요?

밖에 나가서 보면 되죠!

너무 시시하니 예를 들어보죠.

우리는 어떻게 지구가 둥글다는 걸 알까요?

한 바퀴 돌아봐서? 원기둥이었으면 어떡하죠? 도넛 모양이었다면요?

흠… 한 바퀴 돌아 제자리로 올 수 있는 도형은 너무 많네요.

정확한 건 지구 ‘밖’에서 지구를 바라보는 거죠.

그럼 이 생각을 확장해봅시다.

우리가 사는 이 공간 자체가 어떻게 생겼는지 ‘밖’에서 확인할 수 있을까요?

그건 쉽지 않을 것 같아요.

즉, 우리가 찾아야하는 답변은 ‘밖으로 나가지 않고도 어떻게 생겼는지 아는 것’에 있습니다.

저를 가르치셨던 교수님의 표현을 빌리면

미분기하학은 눈을 감고 손바닥으로 더듬더듬 물체를 만져가며 어떻게 생겼는지 아는 것이다.

라고 할 수 있습니다.

여기서 ‘눈을 감는다는 것’은 앞에서 설명한 밖에서 물체를 볼 수 없음을 의미합니다.

그럼 이제 ‘손바닥’과 ‘더듬더듬’의 의미만 알면 되겠네요.

먼저 손바닥부터 보죠.

손바닥이 평면이라고 생각하면 손바닥과 물체는 딱 ‘한 점’에서만 만날 겁니다.

우리는 이걸 ‘접평면’이라고 부르죠.

으잉

접평면… 접선…? 어랍쇼

어 미분 어서오고.

우리는 눈을 감은 상태이기 때문에 아주 넓은 범위를 만져볼 수가 없어요.

내가 콕 집은 한 점 근처만 보는 거죠.

이렇게 작은 범위를 바라보기에 미분은 아주 효과적인 도구입니다.

미분은 구부러져있는 공간을 쫙 펴주거든요.

곡선을 직선(접선), 곡면을 평면(접평면)으로 말이에요.

구부러진 걸 펴주는 건 왜 좋은데?

그건 바로 ‘벡터’를 이용할 수 있다는 거죠.

휘어져있는 공간에서 우리는 벡터를 마음대로 다룰 수가 없어요.

언제 공간 밖으로 날아가 버릴지 모르거든요.

근데 휜 걸 펴주니 벡터를 다룰 수 있게 된 거죠!

자세한 이야기는 나중으로 미룹시다 :)

오케이.. 이제 마지막 ‘더듬더듬’은 뭐야

아직 해결되지 않은 문제는 바로 ‘접평면이 각 점마다 생긴다’는 것입니다.

즉, 조금만 멀리 떨어져도 두 점이 만드는 접평면 사이의 관계를 알 수가 없어요.

그러기 위해서는 손을 떼면 안 되죠.

더듬더듬은 ‘그 주변을 손을 안 떼고 만진다’를 의미합니다.

두 접평면 사이의 관계를 설명할 때에도 미분이 필요합니다.

내가 조금 손바닥을 움직였을 때, 접평면이 얼만큼 기우는지(비율)를 알아야 하니까요!

이게 학부에서 배우는 미분기하학의 개론(?)입니다.

공간 이야기를 하다가 갑자기 물체 표면 얘기로 넘어와서 매끄럽지 않을 수 있습니다.

적당히 잘 확장하는 방법은 기회가 되면 하도록 할게요 ㅎㅎ

일반상대성이론은 밖에서 관측할 수 없는 시공간 자체의 휘어짐을 논하기 위해서 미분기하학의 도움을 받아야만 했습니다.

국소적으로 거리를 재는 metric tensor나, 휘어짐을 표현하는 Riemann tensor같은 개념이 여기에 속하거든요.

제 직관이 도움이 되었기를 바랍니다.

마지막으로 오만한 가우스가 스스로 발견하고도 놀라움을 금치 못했다는 ‘가우스의 빼어난 정리’를 보여드리고 마치겠습니다.

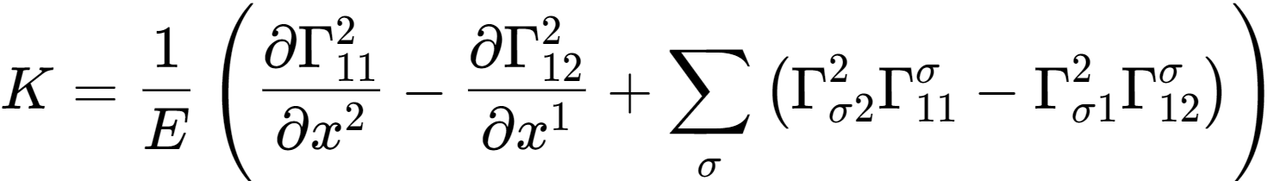
이건 밖에서만 볼 수 있을 줄 알았던 공간의 휘어짐을 공간 내부에서도 알 수 있는 방법을 제시한 가우스의 천재성이 보이는 식입니다.

찡긋